◆問題を含む『オリンピアンの種』を見たい方はコチラから！
【問題】
半径と重さが共通のバスケットボールとボウリング球があります。
これらを同じ斜面の上から転がすとき、早く転がるのはどちらか答えなさい。
ただし、バスケットボールの中身は空洞で、ボウリング球は中まで含め球全体で質量の分布が均一であるものとします。
また、摩擦係数など質量の分布以外の物理的条件は両者で等しいものとします。
（物理チャレンジ2017 予選問題改題）
１：バスケットボール
２：ボウリング球
３：変わらない
【解答/解説】
今のままだと少し状況が複雑なので、もう少し単純な系を考察してみることにします。
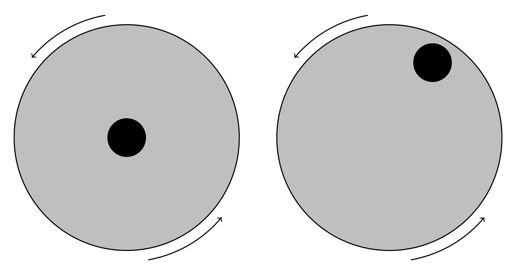
ただし、1つの円盤は中心におもりを置き、もう1つの円盤は縁の方におもりを置くことにします。
このとき、円盤を回すのにより大きなエネルギー（労力）がいるのはどちらでしょうか？ 正解は左側の円盤です。実際、円盤を回しても中心は動かないので、左側は右側に比べておもりを動かさなくていい分「エネルギー的に得をしている」と考えられます。
さて、元の問題に戻ると、考えている2つの球の違いは、質量の分布が均一か外側に偏っているかというところだけでした。上の考察から、中心から離れたところに質量が偏っているとそれを動かすのに余分なエネルギーがかかってしまいますので、より早く転がるのは効率良く動けるボウリング球ということになります。
【解答】２：ボウリング球
余談ですが、例えば球が滑らずに転がるという条件できちんと計算すると、ボウリング球はバスケットボールより25/21倍速く転がるということが分かったりします。これは「剛体の運動方程式」というものを知っていると分かりますが、大学1年生程度の力学の教科書には必ず載っているので、興味がある人はぜひ勉強してみてください。高校物理と微分・積分くらいを知っていれば読めると思います。解説のような初等的考察で問題が解けるのも物理の醍醐味ですが、こんな風にstrictに値を計算できるのもとても魅力的だと個人的には思っています。